Professional Documents
Culture Documents
EM 10 13 Bernoulli
Uploaded by
Dhany SSatOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
EM 10 13 Bernoulli
Uploaded by
Dhany SSatCopyright:
Available Formats
1
Engineering Mathematics
Oct. 13, 2004
2
1.5 Integrating Factors
The equation
is not exact on any rectangle.
Because and
and
=The equation is not exact
on any rectangle.
0 ) 6 3 ( 6
' 2 2
= + y x xy xy y
xy y M 6
2
=
2
6 3 x xy N =
x y xy y
y y
M
6 2 ) 6 (
2
=
c
c
=
c
c
x y x xy
x x
N
12 3 ) 6 3 (
2
=
c
c
=
c
c
x
N
y
M
c
c
=
c
c
3
1.5 Integrating Factor
Recall
Theorem 1.1 Test for Exactness
is exact on
if and only if (),
for each in ,
0 ) , ( ) , (
'
= + y y x N y x M
R
) , ( y x
R
x
N
y
M
c
c
=
c
c
4
1.5 Integrating Factor
If is exact, then there is a
potential function and
and (*)
implicitly defines a function
y(x) that is general solution of the differential
equation.
Thus, finding a function that satisfies
equation(*) is equivalent to solving the
differential equation.
0 ) , ( ) , (
'
= + y y x N y x M
) , (
y x M
x
=
c
c
) , (
y x N
y
=
c
c
( ) C x y x = ) ( ,
5
1.5 Integrating Factor
Definition 1.5
Let and be defined on a region
of a plane. Then is an integrating
factor for if for all
in , and is exact on .
) , ( y x M
) , ( y x N
R
) , ( y x
0
'
= + y N M
0 ) , ( = y x
) , ( y x
R
R 0
'
= + y N M
6
1.5 Integrating Factor
Example 1.21
is not exact.
Here and
For to be an integrating factor,
0
'
= y xy x
xy x M =
1 = N
x xy x
y y
M
=
c
c
=
c
c
) ( 0 ) 1 ( =
c
c
=
c
c
x x
N
) ( ) ( M
y
N
x c
c
=
c
c
( ) ) ( ) ( xy x
y x
c
c
=
c
c
) (
x
y
xy x
x
c
c
=
c
c
7
1.5 Integrating Factor
Example 1.21
For to be an integrating factor,
To simplify the equation, we try to find as
just a function of
This is a separable equation.
) (
x
y
xy x
x
c
c
=
c
c
x
? ) , ( ), ( , ) ( y x y x
0
=
c
c
y
x
x
=
c
c
8
1.2 Separable Equations
A differential equation is called separable
if it can be written as
Such that we can separate the variables
and write
We attempt to integrate this equation
) ( ) (
'
y B x A y =
dx x A dy
y B
) (
) (
1
=
0 ) ( = y B
dx x A dy
y B
) (
) (
1
} }
=
Recall
9
1.5 Integrating Factor
Example 1.21
Integrate to obtain
to get one integrating factor
(*)
The equation (*) is exact over the entire
plane, FOR ALL (x,y) !
x
x
=
c
c
xdx d =
1
xdx d
} }
=
1
C x + =
2
2
1
ln
0
2 /
2
) (
x
e x =
0 ) (
' 2 / 2 /
2 2
= y e e xy x
x x
( )
2 / 2 /
2 2
) (
x x
xe e xy x
y y
M
=
c
c
=
c
c
2 / 2 /
2 2
) (
x x
xe e
x x
N
=
c
c
=
c
c
10
1.5 Integrating Factor
If is exact, then there is a
potential function and
and (*)
implicitly defines a function
y(x) that is general solution of the differential
equation.
Thus, finding a function that satisfies
equation(*) is equivalent to solving the
differential equation.
0 ) , ( ) , (
'
= + y y x N y x M
) , (
y x M
x
=
c
c
) , (
y x N
y
=
c
c
( ) C x y x = ) ( ,
Recall
11
1.5 Integrating Factor
Example 1.21
and
Then we must have
The general solution of the original equation is
0 ) (
' 2 / 2 /
2 2
= y e e xy x
x x
2 /
2
) ( ) , (
x
e xy x y x M
x
= =
c
c
2 /
2
) , (
x
e y x N
y
= =
c
c
) ( ) , (
2 / 2 /
2 2
x h ye dy e y x
x x
+ = =
}
2 /
2
) (
x
e xy x
x
=
c
c
( ) ) ( ) (
' 2 / 2 /
2 2
x h xye x h ye
x
x x
+ = +
c
c
=
2 / '
2
) (
x
xe x h =
2 /
2
) (
x
e x h =
2 /
2
) 1 ( ) , (
x
e y y x =
C e y y x
x
= =
2 /
2
) 1 ( ) , (
2 /
2
1 ) (
x
Ce x y
=
12
1.5.1 Separable Equations and Integrating Factor
The separable equation
is in general not exact. Write it as
and
In general
However,
is an integrating factor for the separable equation.
If we multiply the DE by ,we get
an exact equation. Because
) ( ) (
'
y B x A y =
0 ) ( ) (
'
= y y B x A
| | ) ( ) ( ) ( ) (
'
y B x A y B x A
y y
M
=
c
c
=
c
c
0 ) 1 ( =
c
c
=
c
c
x x
N
0 ) ( ) (
'
= y B x A
) (
1
) (
y B
y =
) (
1
) (
y B
y =
0
) (
1
) (
'
= y
y B
x A
| | 0 ) (
) (
1
=
c
c
=
(
c
c
x A
y y B x
13
1.3 Linear Differential Equations
Linear: A differential equation is called linear if
there are no multiplications among dependent
variables and their derivatives. In other words,
all coefficients are functions of independent
variables.
Non-linear: Differential equations that do not
satisfy the definition of linear are non-linear.
Quasi-linear: For a non-linear differential
equation, if there are no multiplications among
all dependent variables and their derivatives in
the highest derivative term, the differential
equation is considered to be quasi-linear.
) ( ) ( ) (
'
x q y x p x y = +
Recall
14
1.3 Linear Differential Equations
Example 1.14
is a linear DE. P(x)=1 and
q(x)=sin(x), both continuous for all x.
An integrating factor is
Multiply the DE by to get
Or
Integrate to get
The general solution is
) sin(
'
x y y = +
x
dx
dx x p
e e e = =
}
}
) (
x
e ) sin(
'
x e ye e y
x x x
= +
( ) ) sin(
'
x e ye
x x
=
| | C x x e dx x e ye
x
x x
+ = =
}
) cos( ) sin(
2
1
) sin(
| |
x
Ce x x y
+ = ) cos( ) sin(
2
1
Recall
15
1.5.2 Linear Equations and Integrating Factor
The linear equation
Write it as
and
so the linear equation is not exact
unless
However,
is exact because
) ( ) (
'
x q y x p y = +
| | 0 ) ( ) (
'
= + y x q y x p
| | ) ( ) ( ) ( x p x q y x p
y y
M
=
c
c
=
c
c
| | 0 1 =
c
c
=
c
c
x x
N
0 ) ( = x p
dx x p
e y x
) (
) , (
}
=
| | 0 ) ( ) (
'
) ( ) (
= +
} }
y e e x q y x p
dx x p dx x p
| |
dx x p dx x p dx x p
e x q y x p
y
e x p e
x
) ( ) ( ) (
)] ( ) ( [ ) (
} } }
c
c
= =
c
c
16
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.1 Homogeneous Differential Equations
Definition 1.6.1 Homogeneous Equation
A first-order differential equation is homogeneous if it
has the form
For example: is homogeneous
while is not.
|
.
|
\
|
=
x
y
f y
'
|
.
|
\
|
=
x
y
x
y
y sin
'
y x y
2 '
=
17
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.1 Homogeneous Differential Equations
A homogeneous equation is always transformed into a
separable one by the transformation
and write
Then becomes
And the variables (x, u) have been separated.
ux y =
u x u u x x u y + = + =
' ' ' '
x y u / =
) / (
'
x y f y = ) (
'
u f u x u = +
x dx
du
u u f
1
) (
1
=
dx
x
du
u u f
1
) (
1
=
18
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.1 Homogeneous Differential Equations
Example 1.25
Let y=ux or
the general solution of the transformed equation
the general solution of the original equation
y
x
y
xy + =
2
'
x
y
x
y
y +
|
.
|
\
|
=
2
'
u u u x u + = +
2 '
2 '
u x u =
dx
x
du
u
1 1
2
= C x
u
+ = ln
1
C x
x u
+
=
ln
1
) (
C x
x
y
+
=
ln
19
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.2 The Bernoulli Equations
A Bernoulli equation is a first-order equation
(*) in which is a real number.
If or separable and linear ODE
Let for , then (**)
(*)
(*),(**) linear ODE
'
) ( ) ( y x R y x P y = +
0 =
1
= y v 1 =
dx
dy
y
dx
dv
) 1 (
=
1
) ( ) (
= y x P x R
dx
dy
y ) ( ) (
x vP x R
dx
dy
y =
)] ( ) ( )[ 1 ( x vP x R
dx
dv
=
1 =
20
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.2 The Bernoulli Equations
Example 1.27
which is Bernoulli with , and
Make the change of variables , then
and
so the DE becomes
upon multiplying by
a linear equation
3 2 '
3
1
y x y
x
y = +
x x P / 1 ) ( =
2
3 ) ( x x R =
3 =
'
) ( ) ( y x R y x P y = +
2
= y v
2 / 1
= v y
) (
2
1
) (
' 2 / 3 '
x v v x y
=
2 / 3 2 2 / 1 ' 2 / 3
3
1
) (
2
1
= + v x v
x
x v v
2 / 3
2v
2 '
6
2
) ( x v
x
x v =
21
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.2 The Bernoulli Equations
Example 1.27
a linear equation
An integrating factor is
Integrate to get
The general sol of the Bernoulli equation is
3 2 '
3
1
y x y
x
y = +
2 '
6
2
) ( x v
x
x v =
2 ) ln( 2
) / 2 ( ) (
) , (
= = = =
} }
x e e e y x
x
dx x dx x p
6 2 ) (
3 ' 2
=
v x x v x ( ) 6
'
2
=
v x
C x v x + =
6
2 2 3
6 Cx x v + =
3 2
6
1
) (
1
) (
x Cx x v
x y
= =
22
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.2 The Riccati Equations
Definition 1.8 A differential equation of the form
is called a Riccati equation
A Riccati equation is linearly exactly when
Consider the first-order DE
If we approximate ,while x is kept constant,
How to transform the Riccati equation to a linear one ?
) ( ) ( ) (
2 '
x R y x Q y x P y + + =
0 ) ( = x P
) , ( y x f
dx
dy
=
) , ( y x f
... ) ( ) ( ) ( ) , (
2
+ + + = y x R y x Q x P y x f
23
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.2 The Riccati Equations
How to transform the Riccati equation to a linear one ?
Somehow we get one solution, , of a Riccati
equation, then the change of variables
transforms the Riccati equation to a linear one.
) ( ) ( ) (
2 '
x R y x Q y x P y + + =
) (x S
z
x S y
1
) ( + =
24
1.6 Homogeneous, Bernoulli, and Riccati Equations
1.6.2 The Riccati Equations
Example 1.28
By inspection, , is one solution. Define a new
variable z by the change of variables
Then
Or
a linear equation
x
y
x
y
x
y
2 1 1
2 '
+ =
1 ) ( = = x S y
z
y
1
1+ =
'
2
'
1
z
z
y =
x z x z x
z
z
2 1
1
1 1
1
1 1
2
'
2
|
.
|
\
|
+ +
|
.
|
\
|
+ =
x
z
x
z
1 3
'
=
You might also like
- A-level Maths Revision: Cheeky Revision ShortcutsFrom EverandA-level Maths Revision: Cheeky Revision ShortcutsRating: 3.5 out of 5 stars3.5/5 (8)
- Symmetry & Odd/Even Functions: Example 1: Test The Relation 2y X + 3 For Symmetry About Both The Coordinate AxesDocument4 pagesSymmetry & Odd/Even Functions: Example 1: Test The Relation 2y X + 3 For Symmetry About Both The Coordinate Axesinam vfNo ratings yet
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsFrom EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsNo ratings yet
- Exponential and Logarithmic Functions: Key Properties and GraphsDocument24 pagesExponential and Logarithmic Functions: Key Properties and GraphsChathura LakmalNo ratings yet
- MainDocument42 pagesMainNadine PantiNo ratings yet
- Prelims Introductory Calculus 2012MTDocument22 pagesPrelims Introductory Calculus 2012MTMaoseNo ratings yet
- MATH2015-6A-M-Exact Differential EquationDocument13 pagesMATH2015-6A-M-Exact Differential EquationAli AliNo ratings yet
- DifferentiationDocument44 pagesDifferentiationnaseem113No ratings yet
- 2.7. Special Integrating FactorsDocument3 pages2.7. Special Integrating Factorsuchiha_rhenzakiNo ratings yet
- Solving Linear First-Order ODEs Using Integrating FactorsDocument3 pagesSolving Linear First-Order ODEs Using Integrating FactorsMycon EchanoNo ratings yet
- CH 2.6: Exact Equations & Integrating Factors: y y X N y X MDocument10 pagesCH 2.6: Exact Equations & Integrating Factors: y y X N y X MOmegle ConvosNo ratings yet
- First-Order OdesDocument25 pagesFirst-Order OdesMohammad Al-amariNo ratings yet
- Actsc 432 Review Part 1Document7 pagesActsc 432 Review Part 1osiccorNo ratings yet
- Exam P Formula SheetDocument14 pagesExam P Formula SheetToni Thompson100% (4)
- Lecture 09Document15 pagesLecture 09nandish mehtaNo ratings yet
- Ordinary Differential EquationDocument73 pagesOrdinary Differential EquationWahyu SutrisnoNo ratings yet
- Chapter 6: Integration: Partial Fractions and Improper IntegralsDocument33 pagesChapter 6: Integration: Partial Fractions and Improper IntegralsAriana HallNo ratings yet
- Differential Equations BasicsDocument9 pagesDifferential Equations BasicsMarielle Lucas GabrielNo ratings yet
- Functions 1.15 AssesmentDocument14 pagesFunctions 1.15 AssesmentbriNo ratings yet
- Chapter 6F-PropCRV - W PDFDocument30 pagesChapter 6F-PropCRV - W PDFaltwirqiNo ratings yet
- Math 312 Lecture Notes Linearization: Warren Weckesser Department of Mathematics Colgate University 23 March 2005Document8 pagesMath 312 Lecture Notes Linearization: Warren Weckesser Department of Mathematics Colgate University 23 March 2005Dikki Tesna SNo ratings yet
- Math 1Document86 pagesMath 1Naji ZaidNo ratings yet
- Mat 217 Group 7 EXACT DIFFERENTIAL EQUATIONDocument5 pagesMat 217 Group 7 EXACT DIFFERENTIAL EQUATIONOlonade TeniolaNo ratings yet
- Solving Higher Order Linear Differential EquationsDocument56 pagesSolving Higher Order Linear Differential EquationsAna CristacheNo ratings yet
- Ebook Course in Probability 1St Edition Weiss Solutions Manual Full Chapter PDFDocument63 pagesEbook Course in Probability 1St Edition Weiss Solutions Manual Full Chapter PDFAnthonyWilsonecna100% (5)
- Quantum Mechanics Math ReviewDocument5 pagesQuantum Mechanics Math Reviewstrumnalong27No ratings yet
- Linear Differential EquationsDocument30 pagesLinear Differential Equationsshivam12365No ratings yet
- Financial Engineering & Risk Management: Review of Basic ProbabilityDocument46 pagesFinancial Engineering & Risk Management: Review of Basic Probabilityshanky1124No ratings yet
- Topical Revision Notes Additional Mathematics O Level PDFDocument186 pagesTopical Revision Notes Additional Mathematics O Level PDFShamvil Raza100% (5)
- Correlation in Random VariablesDocument6 pagesCorrelation in Random VariablesMadhu Babu SikhaNo ratings yet
- Derivatives of Algebraic Functions Theorems On Differentiation of Algebraic Functions and Higher-Order DerivativesDocument12 pagesDerivatives of Algebraic Functions Theorems On Differentiation of Algebraic Functions and Higher-Order DerivativeshappyfacerocksNo ratings yet
- Differential EquationsDocument8 pagesDifferential EquationsJong CruzNo ratings yet
- Differentiation of Exponential FunctionsDocument20 pagesDifferentiation of Exponential FunctionsPrya Suthan SathiananthanNo ratings yet
- MAS 201 Spring 2021 (CD) Chapter 3 Higher-Order Differential EquationsDocument23 pagesMAS 201 Spring 2021 (CD) Chapter 3 Higher-Order Differential EquationsBlue horseNo ratings yet
- First-Order Differential EquationsDocument30 pagesFirst-Order Differential EquationskakaNo ratings yet
- Everyman Diff Eq'sDocument86 pagesEveryman Diff Eq'sNicholas CemenenkoffNo ratings yet
- An Introduction to Differential Equations: Basic Concepts, ODE vs PDE, Order of a Differential Equation, Examples, and Linear Differential EquationsDocument97 pagesAn Introduction to Differential Equations: Basic Concepts, ODE vs PDE, Order of a Differential Equation, Examples, and Linear Differential EquationsAltammar13100% (1)
- Linear Differential Equation J&I PDFDocument77 pagesLinear Differential Equation J&I PDFscribdrayanNo ratings yet
- LSE EC221 Solutions to Problem Set 2Document6 pagesLSE EC221 Solutions to Problem Set 2slyk1993No ratings yet
- Multivariate Normal Distribution: 3.1 Basic PropertiesDocument13 pagesMultivariate Normal Distribution: 3.1 Basic PropertiesGeorge WangNo ratings yet
- Lecture 22Document4 pagesLecture 22praiselovesscienceNo ratings yet
- MATH 4: Solving Differential EquationsDocument7 pagesMATH 4: Solving Differential EquationsHoney Roselle MorenoNo ratings yet
- Binet's Formula Via Generating FunctionDocument4 pagesBinet's Formula Via Generating FunctionMiliyon TilahunNo ratings yet
- Matrix Multiplication ProgramDocument12 pagesMatrix Multiplication Programsachin rawatNo ratings yet
- The Logistic Equation and BifurcationDocument23 pagesThe Logistic Equation and BifurcationAbhishek GambhirNo ratings yet
- Multivariate Normal Distribution: 3.1 Basic PropertiesDocument13 pagesMultivariate Normal Distribution: 3.1 Basic PropertiesApam BenjaminNo ratings yet
- Integral Calculus PDFDocument32 pagesIntegral Calculus PDFShyam MahendraNo ratings yet
- Finite DifferencesDocument24 pagesFinite DifferencesVenkateshVadithyaNo ratings yet
- Lecture 03Document93 pagesLecture 03Atiq rifatNo ratings yet
- Indefinite IntegrationDocument74 pagesIndefinite IntegrationMohammed ShameeriNo ratings yet
- Maths Linear Differential Equation BSC 2semseterDocument18 pagesMaths Linear Differential Equation BSC 2semseterShivamNo ratings yet
- Functions - Topic 1Document23 pagesFunctions - Topic 1oliverosmarkfeNo ratings yet
- Physics LabDocument80 pagesPhysics LabPriyanshu KumarNo ratings yet
- 5 Linear First Order EquationsDocument10 pages5 Linear First Order EquationsFurkan ErdenNo ratings yet
- Ee1010a 03Document13 pagesEe1010a 03林凱文No ratings yet
- Solving Linear Differential EquationsDocument52 pagesSolving Linear Differential Equationsferrer24No ratings yet
- Expectation: Moments of A DistributionDocument39 pagesExpectation: Moments of A DistributionDaniel Lee Eisenberg JacobsNo ratings yet
- 002 - Exact First Order DEDocument12 pages002 - Exact First Order DEKuroha KokonoseNo ratings yet
- 2.4 Non Exact Differential Equations - Hand OutDocument14 pages2.4 Non Exact Differential Equations - Hand OutFranz Hendrix GagarinNo ratings yet
- Improper Integrals Involving Rational and Exponential Functions PDFDocument10 pagesImproper Integrals Involving Rational and Exponential Functions PDFhammoudeh13No ratings yet
- Precision Refrigeration Ammonia Training: Mechanical IntegrityDocument17 pagesPrecision Refrigeration Ammonia Training: Mechanical IntegrityDhany SSatNo ratings yet
- ResumeDocument11 pagesResumeJoey Cross fxNo ratings yet
- MFFS - BC MultiFunctionFoamSpray PInfo ENDocument1 pageMFFS - BC MultiFunctionFoamSpray PInfo ENDhany SSatNo ratings yet
- Detail Model Pondasi Batu Kali Detail Model Cakar Ayam: Otosat Engineering NO. 007/II/CIV/2021 Otosat EngineeringDocument1 pageDetail Model Pondasi Batu Kali Detail Model Cakar Ayam: Otosat Engineering NO. 007/II/CIV/2021 Otosat EngineeringDhany SSatNo ratings yet
- VIC - BC ValvesandInjectionSystemCleaner PInfo ENDocument1 pageVIC - BC ValvesandInjectionSystemCleaner PInfo ENDhany SSatNo ratings yet
- Simple Guitar Fuzz Effect Circuit Using IC-741 - Electronic Projects CircuitsDocument6 pagesSimple Guitar Fuzz Effect Circuit Using IC-741 - Electronic Projects CircuitsDhany SSatNo ratings yet
- Carbon X Combustion Chamber Cleaner K1+K2Document2 pagesCarbon X Combustion Chamber Cleaner K1+K2Dhany SSatNo ratings yet
- Carbon X Combustion Chamber Cleaner K1+KDocument2 pagesCarbon X Combustion Chamber Cleaner K1+KDhany SSatNo ratings yet
- Daftar Setting Satelit MatrixDocument2 pagesDaftar Setting Satelit MatrixDhany SSatNo ratings yet
- Oxygen Sensor & Catalytic Converter CleanerDocument1 pageOxygen Sensor & Catalytic Converter CleanerDhany SSatNo ratings yet
- American Tool Pricelist CatalogueDocument6 pagesAmerican Tool Pricelist CatalogueDhany SSatNo ratings yet
- Robot Axis Control Using Brushless DC Motor Drive - MATLAB & SimulinkDocument11 pagesRobot Axis Control Using Brushless DC Motor Drive - MATLAB & SimulinkDhany SSatNo ratings yet
- Contact BasecampDocument1 pageContact BasecampDhany SSatNo ratings yet
- Timex Watch Repair Service Centers IndonesiaDocument1 pageTimex Watch Repair Service Centers IndonesiaDhany SSatNo ratings yet
- Project Open Hand Material 3D Print: No Name File Part Qty Position File To PartDocument1 pageProject Open Hand Material 3D Print: No Name File Part Qty Position File To PartDhany SSatNo ratings yet
- Company Name: Business Plan PresentationDocument12 pagesCompany Name: Business Plan PresentationDhany SSatNo ratings yet
- Comitment Customer - After Sales DevelopmentDocument8 pagesComitment Customer - After Sales DevelopmentDhany SSatNo ratings yet
- Applicastatus File Ty File Se File Se File NbregistrpublicatitleDocument16 pagesApplicastatus File Ty File Se File Se File NbregistrpublicatitleDhany SSatNo ratings yet
- Eagle SwitchingPLC PCBtinyR002Document1 pageEagle SwitchingPLC PCBtinyR002Dhany SSatNo ratings yet
- Popular Science 2010-03Document97 pagesPopular Science 2010-03Dhany SSat100% (1)
- Electromyography, Myoelectric Signals and Their Use in Controlling Prosthetic LimbsDocument22 pagesElectromyography, Myoelectric Signals and Their Use in Controlling Prosthetic LimbsMohamed Ahmed NaderNo ratings yet
- Sejarah Formula ReyNolds R ARFM 90Document13 pagesSejarah Formula ReyNolds R ARFM 90Dhany SSatNo ratings yet
- Customer Engagement Capitalize RepesentativeDocument14 pagesCustomer Engagement Capitalize RepesentativeDhany SSatNo ratings yet
- Breaking The 1 Teraflop Barrier: Amd Firestream 9250Document2 pagesBreaking The 1 Teraflop Barrier: Amd Firestream 9250Dhany SSatNo ratings yet
- Preesure ComputerDocument1 pagePreesure ComputerDhany SSatNo ratings yet
- Fracture MechanicsDocument31 pagesFracture MechanicsDhany SSat100% (2)
- Part Civic 1977Document5 pagesPart Civic 1977Dhany SSatNo ratings yet
- Madu Nau NayDocument1 pageMadu Nau NayDhany SSatNo ratings yet
- Proposal Turnamen Golf 82Document8 pagesProposal Turnamen Golf 82Dhany SSatNo ratings yet
- Disturbance Force ROVDocument1 pageDisturbance Force ROVDhany SSatNo ratings yet
- Linear EquationsDocument25 pagesLinear EquationsOrestes MendozaNo ratings yet
- Math Jingle Rap (Linear Functions and Equations)Document2 pagesMath Jingle Rap (Linear Functions and Equations)Karen Juan60% (5)
- Homework 3: ANSWERS provides infinitely many solutionsDocument4 pagesHomework 3: ANSWERS provides infinitely many solutionskrishnaNo ratings yet
- Chapter 2 Quadratic FunctionsDocument2 pagesChapter 2 Quadratic FunctionsWan HasliraNo ratings yet
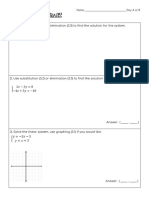
- Integrated: 3.1 - 3.3 QUIZ!!: Name - Day: A or BDocument2 pagesIntegrated: 3.1 - 3.3 QUIZ!!: Name - Day: A or BDalton PatnodeNo ratings yet
- Solutions To Homework 5, Jackson E&m, For Graduate E&m Physics ClassDocument6 pagesSolutions To Homework 5, Jackson E&m, For Graduate E&m Physics ClassAnna Wu100% (1)
- EquilibriumDocument20 pagesEquilibriumShandy Nurmansyah100% (1)
- Signals and Systems Quiz SolutionsDocument18 pagesSignals and Systems Quiz SolutionsIbrahim QahtanNo ratings yet
- Systems of Two EquationsDocument4 pagesSystems of Two Equationsapi-253892365No ratings yet
- MATH115 Course PackDocument20 pagesMATH115 Course PackronieNo ratings yet
- Solution of Differential EquationsDocument34 pagesSolution of Differential EquationsSaddie SoulaNo ratings yet
- 12 Homotopy Perturbation Method: A (u) − f (r) =, r ∈ ΩDocument9 pages12 Homotopy Perturbation Method: A (u) − f (r) =, r ∈ ΩReza SadeghiNo ratings yet
- Table A.2: Coefficients C For Orthogonal Polynomial Trend ContrastsDocument1 pageTable A.2: Coefficients C For Orthogonal Polynomial Trend ContrastsYONATAN STIVEN HOYOS SERNANo ratings yet
- Mains Fundamental of Algebraic - Expression - Paper-01Document4 pagesMains Fundamental of Algebraic - Expression - Paper-01Sanjay GuptaNo ratings yet
- IGCSE H2 07b 04 Quadratic FormulaDocument1 pageIGCSE H2 07b 04 Quadratic FormulaPratham MinochaNo ratings yet
- Least Learned Competencies First Quarter: Grade 9 MathematicsDocument2 pagesLeast Learned Competencies First Quarter: Grade 9 MathematicsStevenson Tugade VelascoNo ratings yet
- 1 MT-102Document2 pages1 MT-102RaviNo ratings yet
- Solution Agrawal Cap 2Document2 pagesSolution Agrawal Cap 2Loren Forero100% (1)
- PolynomialDocument4 pagesPolynomialDennis ANo ratings yet
- Math Grade 9Document5 pagesMath Grade 9J Randolf Silvestre100% (2)
- Dynamics 2Document55 pagesDynamics 2Ahmed MandorNo ratings yet
- Chapter 9 - Numerical Methods For 1D Unsteady Heat & Wave EquationsDocument60 pagesChapter 9 - Numerical Methods For 1D Unsteady Heat & Wave EquationsAjayNo ratings yet
- MA 542 - Differential Equations: End-Semester Examination Department of MathematicsDocument2 pagesMA 542 - Differential Equations: End-Semester Examination Department of MathematicsNaveen GuptaNo ratings yet
- Finite Element AnDocument2 pagesFinite Element AnShreeshaBharadwajNo ratings yet
- Algebra 2 Ans PDFDocument2 pagesAlgebra 2 Ans PDFPuja AgarwalNo ratings yet
- Lecture Notes 10 5Document12 pagesLecture Notes 10 5uncle wizNo ratings yet
- Rev Vectors Paper 1 MSDocument13 pagesRev Vectors Paper 1 MSmac richNo ratings yet
- L08 - Multi-Grid MethodsDocument54 pagesL08 - Multi-Grid MethodsSulaiman AL MajdubNo ratings yet
- An Introduction To The Split Step Fourier Method Using MATLABDocument15 pagesAn Introduction To The Split Step Fourier Method Using MATLABHafiz Faiz RasoolNo ratings yet
- Third Order ODE ExampleDocument2 pagesThird Order ODE ExampleBuiThaiChienNo ratings yet