Professional Documents
Culture Documents
Complete Business Statistics: by Amir D. Aczel & Jayavel Sounderpandian 6 Edition (SIE)
Uploaded by
ArunkumarOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Complete Business Statistics: by Amir D. Aczel & Jayavel Sounderpandian 6 Edition (SIE)
Uploaded by
ArunkumarCopyright:
Available Formats
5-1
COMPLETE
BUSINESS
STATISTICS
by
AMIR D. ACZEL
&
JAYAVEL SOUNDERPANDIAN
6
th
edition (SIE)
5-2
Chapter 5
Sampling and Sampling
Distributions
5-3
Using Statistics
Sample Statistics as Estimators of
Population Parameters
Sampling Distributions
Estimators and Their Properties
Degrees of Freedom
The Template
Sampling and Sampling Distributions
5
5-4
Take random samples from populations
Distinguish between population parameters and sample statistics
Apply the central limit theorem
Derive sampling distributions of sample means and proportions
Explain why sample statistics are good estimators of population
parameters
Judge one estimator as better than another based on desirable
properties of estimators
Apply the concept of degrees of freedom
Identify special sampling methods
Compute sampling distributions and related results using
templates
LEARNING OBJECTIVES
5
After studying this chapter you should be able to:
5-5
Statistical Inference:
Predict and forecast values of
population parameters...
Test hypotheses about values
of population parameters...
Make decisions...
On basis of sample statistics
derived from limited and
incomplete sample
information
Make generalizations
about the
characteristics of a
population...
On the basis of
observations of a
sample, a part of a
population
5-1 Using Statistics
5-6
Democrats
Republicans
People who have
phones and/or cars
and/or are Digest
readers.
Biased
Sample
Population
Democrats
Republicans
Unbiased
Sample
Population
Unbiased,
representative sample
drawn at random from
the entire population.
Biased,
unrepresentative
sample drawn from
people who have cars
and/or telephones
and/or read the Digest.
The Literary Digest Poll (1936)
5-7
An estimator of a population parameter is a sample statistic
used to estimate or predict the population parameter.
An estimate of a parameter is a particular numerical value
of a sample statistic obtained through sampling.
A point estimate is a single value used as an estimate of a
population parameter.
A population parameter
is a numerical measure of
a summary characteristic
of a population.
5-2 Sample Statistics as Estimators of
Population Parameters
A sample statistic is a
numerical measure of a
summary characteristic
of a sample.
5-8
The sample mean, , is the most common
estimator of the population mean, .
The sample variance, s
2
, is the most common
estimator of the population variance, o
2
.
The sample standard deviation, s, is the most
common estimator of the population standard
deviation, o.
The sample proportion, , is the most common
estimator of the population proportion, p.
Estimators
X
p
5-9
The population proportion is equal to the number of
elements in the population belonging to the category of
interest, divided by the total number of elements in the
population:
The sample proportion is the number of elements in the
sample belonging to the category of interest, divided by the
sample size:
Population and Sample Proportions
$ p
x
n
=
p
X
N
=
5-10
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
X
Population mean ()
Sample points
Frequency distribution
of the population
Sample mean ( )
A Population Distribution, a Sample from a
Population, and the Population and Sample Means
X
5-11
Stratified sampling: in stratified sampling, the
population is partitioned into two or more
subpopulation called strata, and from each stratum
a desired sample size is selected at random.
Cluster sampling: in cluster sampling, a random
sample of the strata is selected and then samples
from these selected strata are obtained.
Systemic sampling: in systemic sampling, we start
at a random point in the sampling frame, and from
this point selected every k
th
, say, value in the frame
to formulate the sample.
Other Sampling Methods
5-12
The sampling distribution of a statistic is the
probability distribution of all possible values the
statistic may assume, when computed from
random samples of the same size, drawn from a
specified population.
The sampling distribution of X is the
probability distribution of all possible values the
random variable may assume when a sample
of size n is taken from a specified population.
X
5-3 Sampling Distributions
5-13
Uniform population of integers from 1 to 8:
X P(X) XP(X) (X-
x
) (X-
x
)
2
P(X)(X-
x
)
2
1 0.125 0.125 -3.5 12.25 1.53125
2 0.125 0.250 -2.5 6.25 0.78125
3 0.125 0.375 -1.5 2.25 0.28125
4 0.125 0.500 -0.5 0.25 0.03125
5 0.125 0.625 0.5 0.25 0.03125
6 0.125 0.750 1.5 2.25 0.28125
7 0.125 0.875 2.5 6.25 0.78125
8 0.125 1.000 3.5 12.25 1.53125
1.000 4.500 5.25000
8 7 6 5 4 3 2 1
0 . 2
0 . 1
0 . 0
X
P
(
X
)
U n i f o r m D i s t r i b u t i o n ( 1 , 8 )
E(X) = = 4.5
V(X) = o
2
= 5.25
SD(X) = o = 2.2913
Sampling Distributions (Continued)
5-14
There are 8*8 = 64 different but
equally-likely samples of size 2
that can be drawn (with
replacement) from a uniform
population of the integers from 1
to 8:
Samples of Size 2 from Uniform (1,8)
1 2 3 4 5 6 7 8
1 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8
2 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8
3 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8
4 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8
5 5,1 5,2 5,3 5,4 5,5 5,6 5,7 5,8
6 6,1 6,2 6,3 6,4 6,5 6,6 6,7 6,8
7 7,1 7,2 7,3 7,4 7,5 7,6 7,7 7,8
8 8,1 8,2 8,3 8,4 8,5 8,6 8,7 8,8
Each of these samples has a sample
mean. For example, the mean of the
sample (1,4) is 2.5, and the mean of
the sample (8,4) is 6.
Sample Means from Uniform (1,8), n = 2
1 2 3 4 5 6 7 8
1 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
2 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
3 2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5
4 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0
5 3.0 3.5 4.0 4.5 5.0 5.5 6.0 6.5
6 3.5 4.0 4.5 5.0 5.5 6.0 6.5 7.0
7 4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5
8 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0
Sampling Distributions (Continued)
5-15
Sampling Distribution of the Mean
The probability distribution of the sample mean is called the
sampling distribution of the the sample mean.
8 . 0 7 . 5 7 . 0 6 . 5 6 . 0 5 . 5 5 . 0 4 . 5 4 . 0 3 . 5 3 . 0 2 . 5 2 . 0 1 . 5 1 . 0
0 . 1 0
0 . 0 5
0 . 0 0
X
P
(
X
)
S a m p l i n g D i s t r i b u t i o n o f t h e M e a n
X P(X) XP(X) X-
X
(X-
X
)
2
P(X)(X-
X
)
2
1.0 0.015625 0.015625 -3.5 12.25 0.191406
1.5 0.031250 0.046875 -3.0 9.00 0.281250
2.0 0.046875 0.093750 -2.5 6.25 0.292969
2.5 0.062500 0.156250 -2.0 4.00 0.250000
3.0 0.078125 0.234375 -1.5 2.25 0.175781
3.5 0.093750 0.328125 -1.0 1.00 0.093750
4.0 0.109375 0.437500 -0.5 0.25 0.027344
4.5 0.125000 0.562500 0.0 0.00 0.000000
5.0 0.109375 0.546875 0.5 0.25 0.027344
5.5 0.093750 0.515625 1.0 1.00 0.093750
6.0 0.078125 0.468750 1.5 2.25 0.175781
6.5 0.062500 0.406250 2.0 4.00 0.250000
7.0 0.046875 0.328125 2.5 6.25 0.292969
7.5 0.031250 0.234375 3.0 9.00 0.281250
8.0 0.015625 0.125000 3.5 12.25 0.191406
1.000000 4.500000 2.625000
E X
V X
SD X
X
X
X
( )
( )
( ) .
= =
= =
= =
o
o
4. 5
2. 625
1 6202
2
Sampling Distributions (Continued)
5-16
Comparing the population
distribution and the sampling
distribution of the mean:
The sampling distribution is
more bell-shaped and
symmetric.
Both have the same center.
The sampling distribution of
the mean is more compact, with
a smaller variance.
8 7 6 5 4 3 2 1
0 . 2
0 . 1
0 . 0
X
P
(
X
)
U n i f o r m D i s t r i b u t i o n ( 1 , 8 )
X
8 . 0 7 . 5 7 . 0 6 . 5 6 . 0 5 . 5 5 . 0 4 . 5 4 . 0 3 . 5 3 . 0 2 . 5 2 . 0 1 . 5 1 . 0
0 . 1 0
0 . 0 5
0 . 0 0
P
(
X
)
S a m p l i n g D i s t r i b u t i o n o f t h e M e a n
Properties of the Sampling Distribution
of the Sample Mean
5-17
The expected value of the sample mean is equal to the population mean:
E X
X X
( ) = =
The variance of the sample mean is equal to the population variance divided by
the sample size:
V X
n
X
X
( ) = = o
o
2
2
The standard deviation of the sample mean, known as the standard error of
the mean, is equal to the population standard deviation divided by the square
root of the sample size:
SD X
n
X
X
( ) = = o
o
Relationships between Population Parameters and
the Sampling Distribution of the Sample Mean
5-18
When sampling from a normal population with mean and standard
deviation o, the sample mean, X, has a normal sampling distribution:
X N
n
~ ( , )
o
2
This means that, as the
sample size increases, the
sampling distribution of the
sample mean remains
centered on the population
mean, but becomes more
compactly distributed around
that population mean
Normal population
0 . 4
0 . 3
0 . 2
0 . 1
0 . 0
f
(
X
)
S a m p l i n g D i s t r i b u t i o n o f t h e S a m p l e M e a n
Sampling Distribution: n = 2
Sampling Distribution: n =16
Sampling Distribution: n = 4
Sampling from a Normal Population
Normal population
5-19
When sampling from a population
with mean and finite standard
deviation o, the sampling
distribution of the sample mean will
tend to a normal distribution with
mean and standard deviation as
the sample size becomes large
(n >30).
For large enough n:
o
n
) / , ( ~
2
n N X o
P
(
X
)
X
0 . 2 5
0 . 2 0
0 . 1 5
0 . 1 0
0 . 0 5
0 . 0 0
n = 5
P
(
X
)
0 . 2
0 . 1
0 . 0
X
n = 20
f
(
X
)
X
-
0 . 4
0 . 3
0 . 2
0 . 1
0 . 0
Large n
The Central Limit Theorem
5-20
Normal Uniform Skewed
Population
n = 2
n = 30
X X X X
General
The Central Limit Theorem Applies to
Sampling Distributions from Any Population
5-21
Mercury makes a 2.4 liter V-6 engine, the Laser XRi, used in speedboats.
The companys engineers believe the engine delivers an average power of
220 horsepower and that the standard deviation of power delivered is 15 HP.
A potential buyer intends to sample 100 engines (each engine is to be run a
single time). What is the probability that the sample mean will be less than
217HP?
P X P
X
n n
P Z P Z
P Z
( )
( ) .
< =
<
|
\
|
.
|
|
|
= <
|
\
|
.
|
|
|
= <
|
\
|
.
|
|
|
= < =
217
217
217 220
15
100
217 220
15
10
2 0 0228
o
o
The Central Limit Theorem
(Example 5-1)
5-22
Example 5-2
EPS Mean Distribution
0
5
10
15
20
25
Range
F
r
e
q
u
e
n
c
y
2.00 - 2.49
2.50 - 2.99
3.00 - 3.49
3.50 - 3.99
4.00 - 4.49
4.50 - 4.99
5.00 - 5.49
5.50 - 5.99
6.00 - 6.49
6.50 - 6.99
7.00 - 7.49
7.50 - 7.99
5-23
If the population standard deviation, o, is unknown, replace o with
the sample standard deviation, s. If the population is normal, the
resulting statistic:
has a t distribution with (n - 1) degrees of freedom.
The t is a family of bell-shaped and symmetric
distributions, one for each number of degree of
freedom.
The expected value of t is 0.
The variance of t is greater than 1, but approaches
1 as the number of degrees of freedom increases.
The t is flatter and has fatter tails than does the
standard normal.
The t distribution approaches a standard normal
as the number of degrees of freedom increases.
n s
X
t
/
=
Standard normal
t, df=20
t, df=10
0
Students t Distribution
5-24
The sample proportion is the percentage of
successes in n binomial trials. It is the
number of successes, X, divided by the
number of trials, n.
$ p
X
n
=
As the sample size, n, increases, the sampling
distribution of approaches a normal
distribution with mean p and standard
deviation
$ p
p p
n
( ) 1
Sample proportion:
1 5 1 4 1 3 1 2 1 1 1 0 9 8 7 6 5 4 3 2 1 0
0 . 2
0 . 1
0 . 0
P
(
X
)
n = 1 5 , p = 0 . 3
X
14
15
13
15
12
15
11
15
10
15
9
15
8
15
7
15
6
15
5
15
4
15
3
15
2
15
1
15
0
15
15
15
^ p
2 1 0
0 .5
0 .4
0 .3
0 .2
0 .1
0 .0
X
P
(
X
)
n = 2 , p = 0 . 3
1 0 9 8 7 6 5 4 3 2 1 0
0 . 3
0 . 2
0 . 1
0 . 0
P
(
X
)
n=10,p=0.3
X
The Sampling Distribution of the
Sample Proportion,
$ p
5-25
In recent years, convertible sports coupes have become very popular in Japan. Toyota is
currently shipping Celicas to Los Angeles, where a customizer does a roof lift and ships
them back to Japan. Suppose that 25% of all Japanese in a given income and lifestyle
category are interested in buying Celica convertibles. A random sample of 100
Japanese consumers in the category of interest is to be selected. What is the probability
that at least 20% of those in the sample will express an interest in a Celica convertible?
n
p
np E p
p p
n
V p
p p
n
SD p
=
=
= = =
= = =
= = =
100
0 25
100 0 25 25
1 25 75
100
0 001875
1
0 001875 0 04330127
.
( )( . ) ( $ )
( ) (. )(. )
. ( $ )
( )
. . ( $ )
P p P
p p
p p
n
p
p p
n
P z P z
P z
( $ . )
$
( )
.
( )
. .
(. )(. )
.
.
( . ) .
> =
>
= >
= >
= > =
|
\
|
.
|
|
|
|
\
|
.
|
|
|
|
\
|
.
|
0 20
1
20
1
20 25
25 75
100
05
0433
1 15 0 8749
Sample Proportion (Example 5-3)
5-26
An estimator of a population parameter is a sample statistic used to
estimate the parameter. The most commonly-used estimator of the:
Population Parameter Sample Statistic
Mean () is the Mean (X)
Variance (o
2
) is the Variance (s
2
)
Standard Deviation (o) is the Standard Deviation (s)
Proportion (p) is the Proportion ( )
$ p
Desirable properties of estimators include:
Unbiasedness
Efficiency
Consistency
Sufficiency
5-4 Estimators and Their Properties
5-27
An estimator is said to be unbiased if its expected value is equal to
the population parameter it estimates.
For example, E(X)=, so the sample mean is an unbiased estimator of
the population mean. Unbiasedness is an average or long-run
property. The mean of any single sample will probably not equal the
population mean, but the average of the means of repeated
independent samples from a population will equal the population
mean.
Any systematic deviation of the estimator from the population
parameter of interest is called a bias.
Unbiasedness
5-28
An unbiased estimator is on
target on average.
A biased estimator is
off target on average.
{
Bias
Unbiased and Biased Estimators
5-29
An estimator is efficient if it has a relatively small variance (and
standard deviation).
An efficient estimator is,
on average, closer to the
parameter being estimated..
An inefficient estimator is, on
average, farther from the
parameter being estimated.
Efficiency
5-30
An estimator is said to be consistent if its probability of being close
to the parameter it estimates increases as the sample size increases.
An estimator is said to be sufficient if it contains all the information
in the data about the parameter it estimates.
n = 100
n = 10
Consistency
Consistency and Sufficiency
5-31
For a normal population, both the sample mean and
sample median are unbiased estimators of the
population mean, but the sample mean is both more
efficient (because it has a smaller variance), and
sufficient. Every observation in the sample is used in
the calculation of the sample mean, but only the middle
value is used to find the sample median.
In general, the sample mean is the best estimator of the
population mean. The sample mean is the most
efficient unbiased estimator of the population mean. It
is also a consistent estimator.
Properties of the Sample Mean
5-32
The sample variance (the sum of the squared deviations from the
sample mean divided by (n-1) is an unbiased estimator of the
population variance. In contrast, the average squared deviation
from the sample mean is a biased (though consistent) estimator of the
population variance.
E s E
x x
n
E
x x
n
( )
( )
( )
( )
2
2
2
2
2
1
=
|
\
|
.
|
=
|
\
|
.
|
<
o
o
Properties of the Sample Variance
5-33
Consider a sample of size n=4 containing the following data points:
x
1
=10 x
2
=12 x
3
=16 x
4
=?
and for which the sample mean is:
Given the values of three data points and the sample mean, the
value of the fourth data point can be determined:
x =
x
n
=
+ + +
=
+ + + =
12 14 16
4
4
14
12 14 16
4
56
x
x
x
4
56 12 14 16 =
= x
4
56
x
x
n
= =
14
5-5 Degrees of Freedom
x
4
= 14
5-34
If only two data points and the sample mean are known:
x
1
=10 x
2
=12 x
3
=? x
4
=?
The values of the remaining two data points cannot be uniquely
determined:
x =
x
n
=
+ + +
=
+ + + =
12 14
3
4
4
14
12 14
3
4
56
x x
x x
Degrees of Freedom (Continued)
x =14
5-35
The number of degrees of freedom is equal to the total number of
measurements (these are not always raw data points), less the total
number of restrictions on the measurements. A restriction is a
quantity computed from the measurements.
The sample mean is a restriction on the sample measurements, so
after calculating the sample mean there are only (n-1) degrees of
freedom remaining with which to calculate the sample variance.
The sample variance is based on only (n-1) free data points:
s
x x
n
2
2
1
=
( )
( )
Degrees of Freedom (Continued)
5-36
A sample of size 10 is given below. We are to choose three different numbers from
which the deviations are to be taken. The first number is to be used for the first five
sample points; the second number is to be used for the next three sample points; and
the third number is to be used for the last two sample points.
Example 5-4
Sample # 1 2 3 4 5 6 7 8 9 10
Sample
Point
93 97 60 72 96 83 59 66 88 53
i. What three numbers should we choose in order to minimize the SSD
(sum of squared deviations from the mean).?
Note:
( )
2
= x x SSD
5-37
Solution: Choose the means of the corresponding sample points. These are: 83.6,
69.33, and 70.5.
ii. Calculate the SSD with chosen numbers.
Solution: SSD = 2030.367. See table on next slide for calculations.
iii. What is the df for the calculated SSD?
Solution: df = 10 3 = 7.
iv. Calculate an unbiased estimate of the population variance.
Solution: An unbiased estimate of the population variance is SSD/df = 2030.367/7
= 290.05.
Example 5-4 (continued)
5-38
Example 5-4 (continued)
Sample # Sample Point Mean Deviations Deviation
Squared
1 93 83.6 9.4 88.36
2 97 83.6 13.4 179.56
3 60 83.6 -23.6 556.96
4 72 83.6 -11.6 134.56
5 96 83.6 12.4 153.76
6 83 69.33 13.6667 186.7778
7 59 69.33 -10.3333 106.7778
8 66 69.33 -3.3333 11.1111
9 88 70.5 17.5 306.25
10 53 70.5 -17.5 306.25
SSD 2030.367
SSD/df 290.0524
5-39
Sampling Distribution of a Sample Mean
Using the Template
5-40
Sampling Distribution of a Sample Mean (continued)
Using the Template
5-41
Sampling Distribution of a Sample Proportion
Using the Template
5-42
Using the Template
Sampling Distribution of a Sample Proportion (continued)
5-43
Constructing a sampling distribution of the mean from a uniform
population (n=10) using EXCEL (use RANDBETWEEN(0, 1)
command to generate values to graph):
Histogram of Sample Means
0
50
100
150
200
250
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Sample Means (Class Midpoints)
F
r
e
q
u
e
n
c
y
CLASS MIDPOINT FREQUENCY
0.15 0
0.2 0
0.25 3
0.3 26
0.35 64
0.4 113
0.45 183
0.5 213
0.55 178
0.6 128
0.65 65
0.7 20
0.75 3
0.8 3
0.85 0
999
Using the Computer
You might also like
- Complete Business Statistics: Sampling and Sampling DistributionsDocument49 pagesComplete Business Statistics: Sampling and Sampling Distributionsmallick5051rajatNo ratings yet
- Sampling Distribution of the Mean ExplainedDocument26 pagesSampling Distribution of the Mean ExplainedVarsha PeriwalNo ratings yet
- Lecture 5 - 2 - 2015 - Sampling Distn - FINAL - Complete Version PDFDocument40 pagesLecture 5 - 2 - 2015 - Sampling Distn - FINAL - Complete Version PDFJugal BhojakNo ratings yet
- 04.sampling Distributions of The EstimatorsDocument32 pages04.sampling Distributions of The EstimatorsRegina VazNo ratings yet
- Group 2Document65 pagesGroup 2Fazal McphersonNo ratings yet
- Sampling DistributionDocument22 pagesSampling Distributionumar2040No ratings yet
- Unit 3 (SAMPLE AND SAMPLE DISTRIBUTIONS)Document32 pagesUnit 3 (SAMPLE AND SAMPLE DISTRIBUTIONS)Zara Nabilah100% (2)
- CH 07Document45 pagesCH 07sukhmandhawan88No ratings yet
- SamplingDocument50 pagesSamplinghimaniNo ratings yet
- Ch-5 Aczel ProfDocument43 pagesCh-5 Aczel ProfAmanpreet SinghNo ratings yet
- Unit 3 Sampling and Statistical Inference Chapter - I Sampling DistributionsDocument19 pagesUnit 3 Sampling and Statistical Inference Chapter - I Sampling DistributionsEvelyn KeaneNo ratings yet
- CHAPTER 5 - Sampling Distributions Sections: 5.1 & 5.2: AssumptionsDocument9 pagesCHAPTER 5 - Sampling Distributions Sections: 5.1 & 5.2: Assumptionssound05No ratings yet
- Sampling DistributionDocument13 pagesSampling DistributionBilal AliNo ratings yet
- Brief Lecture NotesDocument13 pagesBrief Lecture NotesNazmul HudaNo ratings yet
- Sampling and Sampling Distribution of Sample MeansDocument7 pagesSampling and Sampling Distribution of Sample MeansrakhshandaNo ratings yet
- Desriptive Statistics - Zarni AmriDocument57 pagesDesriptive Statistics - Zarni AmriAVG2011No ratings yet
- Stats Lecture 07. Sample DistributionDocument36 pagesStats Lecture 07. Sample DistributionShair Muhammad hazaraNo ratings yet
- Interpret Standard Deviation Outlier Rule: Using Normalcdf and Invnorm (Calculator Tips)Document12 pagesInterpret Standard Deviation Outlier Rule: Using Normalcdf and Invnorm (Calculator Tips)maryrachel713No ratings yet
- Standard Error of The Mean Central Limit TheoremDocument21 pagesStandard Error of The Mean Central Limit TheoremASHISH100% (8)
- Error and Uncertainty: General Statistical PrinciplesDocument8 pagesError and Uncertainty: General Statistical Principlesdéborah_rosalesNo ratings yet
- StatisticsDocument211 pagesStatisticsHasan Hüseyin Çakır100% (6)
- Sampling Distributions and Standard Error of the MeanDocument71 pagesSampling Distributions and Standard Error of the Meanasdasdas asdasdasdsadsasddssaNo ratings yet
- KWT 4.ukuran Keragaman Data 2013Document29 pagesKWT 4.ukuran Keragaman Data 2013AndiNo ratings yet
- Engineering Probability & StatisticsDocument30 pagesEngineering Probability & StatisticsKhoa Nguyễn HữuNo ratings yet
- Sampling Distribution: Mrs. Padilla Ap Statstics Chaptr 18Document39 pagesSampling Distribution: Mrs. Padilla Ap Statstics Chaptr 18mushtaque61No ratings yet
- Sampling DistributionDocument15 pagesSampling DistributionSafi SheikhNo ratings yet
- Theory & Problems of Probability & Statistics Murray R. SpiegelDocument89 pagesTheory & Problems of Probability & Statistics Murray R. SpiegelPriya SharmaNo ratings yet
- 11 BS201 Prob and Stat - Ch4Document30 pages11 BS201 Prob and Stat - Ch4knmounika2395100% (1)
- BIOMETRY: The Scientific Method and Statistical TestsDocument51 pagesBIOMETRY: The Scientific Method and Statistical TestsCvhr Srtkn AçikgözNo ratings yet
- Aczel Solution 005Document19 pagesAczel Solution 005aman pasari100% (3)
- Statistics SonDocument39 pagesStatistics SonHuseyn AdigozalovNo ratings yet
- Week 8: Chapter 6: Sampling DistributionsDocument33 pagesWeek 8: Chapter 6: Sampling DistributionsA KNo ratings yet
- Elementary StatisticsDocument22 pagesElementary StatisticsRipkah Vyanee100% (1)
- Sampling and The Sampling DistributionDocument31 pagesSampling and The Sampling Distributionmd1sabeel1ansariNo ratings yet
- CHAPTER3 StatisticDocument40 pagesCHAPTER3 StatisticKhairul NidzamNo ratings yet
- S2 Revision NotesDocument2 pagesS2 Revision NotesimnulNo ratings yet
- Module 2 - Sample - AfterclassDocument36 pagesModule 2 - Sample - AfterclassVanessa WongNo ratings yet
- Introduction to Statistics Sample MeansDocument8 pagesIntroduction to Statistics Sample MeansDeimante MatharooNo ratings yet
- Statistics Chapter 1 SummaryDocument53 pagesStatistics Chapter 1 SummaryKevin AlexanderNo ratings yet
- Random Variable & Probability DistributionDocument48 pagesRandom Variable & Probability DistributionRISHAB NANGIANo ratings yet
- CH 9 NotesDocument67 pagesCH 9 NotesSofie JacksonNo ratings yet
- Population - Entire Group of Individuals About Which We Want Information. Sample - Part of The Population From Which We Actually Collect InformationDocument5 pagesPopulation - Entire Group of Individuals About Which We Want Information. Sample - Part of The Population From Which We Actually Collect Informationlauren smithNo ratings yet
- Sampling InferenceDocument83 pagesSampling InferenceBishnu LamsalNo ratings yet
- Qmt12 Chapter 7 Sampling DistributionsDocument49 pagesQmt12 Chapter 7 Sampling DistributionsRenzo MarquezNo ratings yet
- Random Variable BasicsDocument6 pagesRandom Variable BasicsMoises John SangalangNo ratings yet
- Sampling Distribution-1Document17 pagesSampling Distribution-1Shahjahan DashtiNo ratings yet
- Understanding Sampling Distributions of MeansDocument7 pagesUnderstanding Sampling Distributions of MeansDaryl Vincent RiveraNo ratings yet
- Statistics Sampling DistributionsDocument27 pagesStatistics Sampling DistributionsAwnieAzizanNo ratings yet
- Active Learning Task 8Document7 pagesActive Learning Task 8haptyNo ratings yet
- Click To Add Text Dr. Cemre ErciyesDocument69 pagesClick To Add Text Dr. Cemre ErciyesJade Cemre ErciyesNo ratings yet
- Chapter6 StatsDocument4 pagesChapter6 StatsPoonam NaiduNo ratings yet
- Unit3 InferentialnewDocument36 pagesUnit3 InferentialnewArul JothiNo ratings yet
- Sampling and Sampling DistributionsDocument35 pagesSampling and Sampling DistributionsSiddhant ChawlaNo ratings yet
- Standard DeviationDocument12 pagesStandard DeviationCarlos BustamanteNo ratings yet
- The Practice of Statistic For Business and Economics Is An IntroductoryDocument15 pagesThe Practice of Statistic For Business and Economics Is An IntroductoryuiysdfiyuiNo ratings yet
- Sample Size FormulaDocument13 pagesSample Size FormulaAbhik DasNo ratings yet
- Machine Learning - A Complete Exploration of Highly Advanced Machine Learning Concepts, Best Practices and Techniques: 4From EverandMachine Learning - A Complete Exploration of Highly Advanced Machine Learning Concepts, Best Practices and Techniques: 4No ratings yet
- Statistical Inference in Financial and Insurance Mathematics with RFrom EverandStatistical Inference in Financial and Insurance Mathematics with RNo ratings yet
- Learn Statistics Fast: A Simplified Detailed Version for StudentsFrom EverandLearn Statistics Fast: A Simplified Detailed Version for StudentsNo ratings yet
- Talent Management & Succession PlanningDocument57 pagesTalent Management & Succession PlanningFaisal Abid80% (10)
- HR MANAGEMENT COURSEDocument5 pagesHR MANAGEMENT COURSEArunkumarNo ratings yet
- GE's Talent MachineDocument3 pagesGE's Talent MachineArunkumarNo ratings yet
- The Spread of Innovations in Social Networks: ' BehaDocument6 pagesThe Spread of Innovations in Social Networks: ' BehaArunkumarNo ratings yet
- Young 00 DiffusionDocument20 pagesYoung 00 DiffusionArunkumarNo ratings yet
- Design - Centered Introduction To Aerospace EngineeringDocument79 pagesDesign - Centered Introduction To Aerospace EngineeringArunkumarNo ratings yet
- Freemium 101Document20 pagesFreemium 101michael_lheureux9697No ratings yet
- PornDocument0 pagesPornMinhaz AhmedNo ratings yet
- Accenture The Innovation Death SpiralDocument16 pagesAccenture The Innovation Death Spiralvargh3seNo ratings yet
- Skype and Google Have Lessons For Operators in How To CompeteDocument2 pagesSkype and Google Have Lessons For Operators in How To CompeteArunkumarNo ratings yet
- Disruptive Technologies Pedagogical InnovationDocument14 pagesDisruptive Technologies Pedagogical InnovationArunkumarNo ratings yet
- Social AppsDocument6 pagesSocial AppsArunkumarNo ratings yet
- PornDocument0 pagesPornMinhaz AhmedNo ratings yet
- Skype and Google Have Lessons For Operators in How To CompeteDocument2 pagesSkype and Google Have Lessons For Operators in How To CompeteArunkumarNo ratings yet
- Diffusion of Innovations in Social Networks: Effects of Network StructureDocument6 pagesDiffusion of Innovations in Social Networks: Effects of Network StructureArunkumarNo ratings yet
- Make in India - Challenges Before Defence Manufacturing Indian Defence ReviewDocument19 pagesMake in India - Challenges Before Defence Manufacturing Indian Defence ReviewArunkumarNo ratings yet
- Department of Applied Mathematics Chapter 5. Non-Parametric TestsDocument12 pagesDepartment of Applied Mathematics Chapter 5. Non-Parametric TestsArunkumarNo ratings yet
- Artikel 02Document28 pagesArtikel 02ArunkumarNo ratings yet
- 54 B 5 F 3570 CF 26833 Efd 34632Document12 pages54 B 5 F 3570 CF 26833 Efd 34632ArunkumarNo ratings yet
- Airline EconomicsDocument5 pagesAirline EconomicsArunkumarNo ratings yet
- A Model For Social Networks: Riitta Toivonen, Jukka-Pekka Onnela, Jari Sarama Ki, Jo Rkki Hyvo Nen, Kimmo KaskiDocument10 pagesA Model For Social Networks: Riitta Toivonen, Jukka-Pekka Onnela, Jari Sarama Ki, Jo Rkki Hyvo Nen, Kimmo KaskiBhairav MehtaNo ratings yet
- Social AppsDocument6 pagesSocial AppsArunkumarNo ratings yet
- 2008 TRIZ and Innovation ManagementDocument30 pages2008 TRIZ and Innovation Managementayatapit100% (1)
- Disruptive Threat or Innovative Opportunity - OTTDocument16 pagesDisruptive Threat or Innovative Opportunity - OTTSwati KanojiaNo ratings yet
- Number of Worldwide Social Network Users 2010-2018 - StatisticDocument5 pagesNumber of Worldwide Social Network Users 2010-2018 - StatisticArunkumarNo ratings yet
- Comparative Analysis On International Airline Industry: Cost Approach To Measure An Industrial InefficiencyDocument10 pagesComparative Analysis On International Airline Industry: Cost Approach To Measure An Industrial InefficiencyArunkumarNo ratings yet
- Comparative Analysis On International Airline Industry: Cost Approach To Measure An Industrial InefficiencyDocument10 pagesComparative Analysis On International Airline Industry: Cost Approach To Measure An Industrial InefficiencyArunkumarNo ratings yet
- It's Time For Skype, A Social Network or NotDocument12 pagesIt's Time For Skype, A Social Network or NotArunkumarNo ratings yet
- Market Entry Guide-Turkey 0Document80 pagesMarket Entry Guide-Turkey 0ArunkumarNo ratings yet
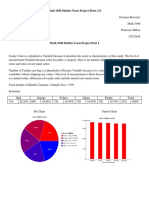
- Skittles Term Project 1-6Document10 pagesSkittles Term Project 1-6api-284733808No ratings yet
- 18.443 MIT Stats CourseDocument139 pages18.443 MIT Stats CourseAditya JainNo ratings yet
- Deconstructing Timbre Into 5 Physiological Parameters: Vocal Mode, Amount of Metal, Degree of Density, Size of Larynx, and Sound ColoringDocument17 pagesDeconstructing Timbre Into 5 Physiological Parameters: Vocal Mode, Amount of Metal, Degree of Density, Size of Larynx, and Sound ColoringOlesea DregleaNo ratings yet
- Statistics and Probability DistributionsDocument5 pagesStatistics and Probability DistributionsJohn ClarenceNo ratings yet
- One Way ANOVADocument11 pagesOne Way ANOVAsaria jabeenNo ratings yet
- Probabilistic Numerics - Part IDocument86 pagesProbabilistic Numerics - Part IConstantin Von TsirlenNo ratings yet
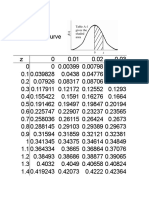
- Table-Standard Normal CDF and Partial ExpectationDocument39 pagesTable-Standard Normal CDF and Partial ExpectationchetanaNo ratings yet
- Exam-Style Question:: Mathematical ModellingDocument4 pagesExam-Style Question:: Mathematical ModellingFadi AyyoubNo ratings yet
- Gradjabbar PDFDocument173 pagesGradjabbar PDFhamid TalibNo ratings yet
- Conducting Ruggedness Tests: Standard Practice ForDocument9 pagesConducting Ruggedness Tests: Standard Practice ForAhmad Zubair Rasuly100% (1)
- Quick User Guide For X Powder XDocument107 pagesQuick User Guide For X Powder XLitarmjNo ratings yet
- Statistics JokesDocument72 pagesStatistics JokesNischit ShettyNo ratings yet
- Chapter IIIDocument4 pagesChapter IIISahsah Spngy50% (2)
- SIPmath Getting StartedDocument10 pagesSIPmath Getting StartedAnanda PrathamaNo ratings yet
- (M7sp-Iva-3) Statistical InstrumentsDocument37 pages(M7sp-Iva-3) Statistical InstrumentsChristine Sapuay Duldulao100% (1)
- Machine Learning RESADocument51 pagesMachine Learning RESAIoanna DiamNo ratings yet
- Latest Social Science Reviewer Part 7Document6 pagesLatest Social Science Reviewer Part 7Rubelin Dagohoy AmitNo ratings yet
- As-AL SOW 9709 06 ProbabilityandStatistics1 S1Document15 pagesAs-AL SOW 9709 06 ProbabilityandStatistics1 S1BalkisNo ratings yet
- SCHM Internship 18feb11Document15 pagesSCHM Internship 18feb11smit1No ratings yet
- Tec482 PDFDocument39 pagesTec482 PDFsaptop39No ratings yet
- Machine Learning Assignment Differences Between Linear And Logistic RegressionDocument4 pagesMachine Learning Assignment Differences Between Linear And Logistic Regressionbharti goyalNo ratings yet
- Measures of Skewness, Kurtosis and MomentsDocument11 pagesMeasures of Skewness, Kurtosis and MomentsBharat ChaudharyNo ratings yet
- Strategic Leadership in The Implementation of County Integrated Development Plan (Cidp) in Busia CountyDocument18 pagesStrategic Leadership in The Implementation of County Integrated Development Plan (Cidp) in Busia Countyrichard achiamboNo ratings yet
- Dynamic Linkages Between Transport, Logistics, Foreign DirectDocument17 pagesDynamic Linkages Between Transport, Logistics, Foreign Directgharsallah imedNo ratings yet
- Multiple Choice QuizDocument3 pagesMultiple Choice QuizRavi Arjun KumarNo ratings yet
- Research - Ashly GroupDocument14 pagesResearch - Ashly GroupRoselyn SalamatNo ratings yet
- COS10022 - Lecture 03 - Data Preparation PDFDocument61 pagesCOS10022 - Lecture 03 - Data Preparation PDFPapersdock TahaNo ratings yet
- Clearing The Fog On Phosphate Rock Data - Uncertainties, Fuzziness, and MisunderstandingsDocument14 pagesClearing The Fog On Phosphate Rock Data - Uncertainties, Fuzziness, and MisunderstandingsDaniel FrancoNo ratings yet
- As of Sep 16, 2020: Seppo Pynn Onen Econometrics IDocument52 pagesAs of Sep 16, 2020: Seppo Pynn Onen Econometrics IorxanmehNo ratings yet
- Working With Research Participants Sampling and EthicsDocument45 pagesWorking With Research Participants Sampling and EthicsJonnel GadinganNo ratings yet