Probability and Statistics

Lecture 8

Dr.-Ing. Erwin Sitompul

President University
http://zitompul.wordpress.com
2 0 1 3
President University

Erwin Sitompul

PBST 8/1

Chapter 6

Some Continuous Probability Distributions

Chapter 6

Some Continuous Probability

Distributions

President University

Erwin Sitompul

PBST 8/2

Chapter 6.1

Continuous Uniform Distribution

Continuous Uniform Distribution

|Uniform Distribution| The density function of the continuous
uniform random variable X on the interval [A, B] is

1
B A , A x B
f ( x; A, B )
0,
elsewhere

The mean and variance of the uniform distribution are

A B

and

( B A) 2

12
2

The uniform density

function for a
random variable on
the interval [1, 3]

President University

Erwin Sitompul

PBST 8/3

Chapter 6.1

Continuous Uniform Distribution

Continuous Uniform Distribution

Suppose that a large conference room for a certain company can be
reserved for no more than 4 hours. However, the use of the
conference room is such that both long and short conference occur
quite often. In fact, it can be assumed that length X of a conference
has a uniform distribution on the interval [0, 4].
(a) What is the probability density function?
(b) What is the probability that any given conference lasts at least 3
hours?

(a)

1
4 , 0 x4
f ( x)
0, elsewhere

(b)

1
1
P X 3 dx
4
4
3

President University

Erwin Sitompul

PBST 8/4

Chapter 6.2

Normal Distribution

Normal Distribution
Normal distribution is the most important continuous probability
distribution in the entire field of statistics.
Its graph, called the normal curve, is the bell-shaped curve which
describes approximately many phenomena that occur in nature,
industry, and research.
The normal distribution is often referred to as the Gaussian
distribution, in honor of Karl Friedrich Gauss, who also derived its
equation from a study of errors in repeated measurements of the
same quantity.

The normal curve

President University

Erwin Sitompul

PBST 8/5

Chapter 6.2

Normal Distribution

Normal Distribution
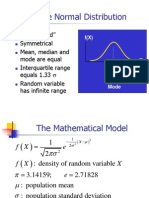
A continuous random variable X having the bell-shaped distribution
as shown on the figure is called a normal random variable.

The density function of the normal random variable X, with mean

and variance 2, is

n( x; , )

1
e
2

1 x

where = 3.14159... and e = 2.71828...

President University

Erwin Sitompul

PBST 8/6

Chapter 6.2

Normal Distribution

Normal Curve

1 < 2, 1 = 2

1 = 2, 1 < 2

1 < 2, 1 < 2
President University

Erwin Sitompul

PBST 8/7

Chapter 6.2

Normal Distribution

Normal Curve
f(x)

The mode, the point where

the curve is at maximum
Concave downward
Point of inflection

Concave upward
Approaches zero
asymptotically

Total area under the curve

and above the horizontal
axis is equal to 1

President University

Symmetry about a vertical

axis through the mean

Erwin Sitompul

PBST 8/8

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

The area under the curve bounded by two ordinates x = x1 and
x = x2 equals the probability that the random variable X assumes
a value between x = x1 and x = x2.

x2

P( x1 X x2 ) n( x; , )dx
x1

President University

Erwin Sitompul

1
2

x2

1 x

dx

x1

PBST 8/9

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

As seen previously, the normal curve is dependent on the mean
and the standard deviation of the distribution under
investigation.
The same interval of a random variable can deliver different
probability if or are different.

Same interval, but different probabilities

for two different normal curves

President University

Erwin Sitompul

PBST 8/10

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

The difficulty encountered in solving integrals of normal density
functions necessitates the tabulation of normal curve area for
quick reference.
Fortunately, we are able to transform all the observations of any
normal random variable X to a new set of observation of a normal
random variable Z with mean 0 and variance 1.

1
2

P( x1 X x2 )

1
2

z2

x2

1 x

dx

x1

z2
2

dz

z1

z2

n( z;0,1)dz P( z1 Z z2 )
z1

President University

Erwin Sitompul

PBST 8/11

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

The distribution of a normal random variable with mean 0 and
variance 1 is called a standard normal distribution.

President University

Erwin Sitompul

PBST 8/12

Chapter 6.3

Areas Under the Normal Curve

Table A.3 Normal Probability Table

President University

Erwin Sitompul

PBST 8/13

Chapter 6.3

Areas Under the Normal Curve

Interpolation
Interpolation is a method of constructing new data points within
the range of a discrete set of known data points.
Examine the following graph. Two data points are known, which
are (a,f(a)) and (b,f(b)).
If a value of c is given, with a < c < b, then the value of f(c) can be
estimated.
If a value of f(c) is given, with f(a) < f(c) < f(b), then the value of c
can be estimated.

f (c ) f ( a )

f (b)

ca
f (b) f (a)
ba

f (c)?
f (a )

c a
a

President University

c?

f (c ) f ( a )
b a
f (b) f (a )

Erwin Sitompul

PBST 8/14

Chapter 6.3

Areas Under the Normal Curve

Interpolation

P(Z < 1.172)?

Answer: 0.8794
P(Z < z) = 0.8700, z = ?
1.126

President University

Erwin Sitompul

PBST 8/15

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

Given a standard normal distribution, find the area under the curve
that lies (a) to the right of z = 1.84 and (b) between z = 1.97 and
z = 0.86.

(a)

P ( Z 1.84) 1 P( Z 1.84)

1 0.9671
0.0329

(b)

P (1.94 Z 0.86) P ( Z 0.86) P( Z 1.94)

0.8051 0.0244
0.7807

President University

Erwin Sitompul

PBST 8/16

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

Given a standard normal distribution, find the value of k such that
(a) P ( Z > k ) = 0.3015, and (b) P ( k < Z < 0.18 ) = 0.4197.

(a)

P( Z k ) 1 P(Z k )

P(Z k ) 1 P( Z k )
1 0.3015 0.6985
k 0.52

(b)

P(k Z 0.18) P( Z 0.18) P( Z k )

P ( Z k ) P( Z 0.18) P(k Z 0.18)

0.4286 0.4197 0.0089

k 2.37
President University

Erwin Sitompul

PBST 8/17

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

Given a random variable X having a normal distribution with = 50
and = 10, find the probability that X assumes a value between 45
and 62.
z1

x1
45 50

0.5

10

z2

x2 62 50

1.2

10

P(45 X 62) P ( 0.5 Z 1.2)

P ( Z 1.2) P ( Z 0.5)
0.8849 0.3085
0.5764

President University

Erwin Sitompul

PBST 8/18

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

Given that X has a normal distribution with = 300 and = 50, find
the probability that X assumes a value greater than 362.
z

x
362 300

1.24

50

P( X 362) P ( Z 1.24)
1 P( Z 1.24)
1 0.8925
0.1075

President University

Erwin Sitompul

PBST 8/19

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

Given a normal distribution with = 40 and = 6, find the value of x
that has (a) 45% of the area to the left, and (b) 14% of the area to
the right.
(a)

P ( Z z ) 0.45

z 0.13

0.45 0.4483
0.12 (0.13) 0.1256
0.4522 0.4483

x z 40 (0.1256)(6) 39.2464

0.4522
0.45
0.4483
President University

0.13

0.12

Erwin Sitompul

PBST 8/20

Chapter 6.3

Areas Under the Normal Curve

Area Under the Normal Curve

Given a normal distribution with = 40 and = 6, find the value of x
that has (a) 45% of the area to the left, and (b) 14% of the area to
the right.
(b)

P ( z Z ) 0.14 1 P( Z z )
P( Z z ) 1 0.14 0.86
z 1.08

x z 40 (1.08)(6) 46.48

President University

Erwin Sitompul

PBST 8/21

Chapter 6.4

Applications of the Normal Distribution

Applications of the Normal Distribution

A certain type of storage battery lasts, on average, 3.0 years, with a
standard deviation of 0.5 year. Assuming that the battery lives are
normally distributed, find the probability that a given battery will last
less than 2.3 years.

x
2.3 3.0

1.4

0.5

P( Z 1.4) 0.0808
8.08%

President University

Erwin Sitompul

PBST 8/22

Chapter 6.4

Applications of the Normal Distribution

Applications of the Normal Distribution

In an industrial process the diameter of a ball bearing is an
important component part. The buyer sets specifications on the
diameter to be 3.0 0.01 cm. All parts falling outside these
specifications will be rejected.
It is known that in the process the diameter of a ball bearing has a
normal distribution with mean 3.0 and standard deviation 0.005.
On the average, how many manufactured ball bearings will be
scrapped?
P (2.99 X 3.01) P(2 Z 2)
P ( Z 2) P ( Z 2)
0.9772 0.0228
0.9544

x1 2.99 3.0

0.005
x 3.01 3.0
z2 2

0.005

95.44% accepted

z1

President University

4.56% rejected
Erwin Sitompul

PBST 8/23

Chapter 6.4

Applications of the Normal Distribution

Applications of the Normal Distribution

A certain machine makes electrical resistors having a mean
resistance of 40 and a standard deviation of 2 . It is assumed
that the resistance follows a normal distribution.
What percentage of resistors will have a resistance exceeding 43
if:
(a) the resistance can be measured to any degree of accuracy.
(b) the resistance can be measured to the nearest ohm only.
(a)

43 40
1.5
2
P ( X 43) P( Z 1.5) 1 P( Z 1.5) 1 0.9332 0.0668 6.68%

(b)

43.5 40
1.75
2
P ( X 43.5) P( Z 1.75) 1 P( Z 1.75) 1 0.9599 0.0401 4.01%

As many as 6.68%4.01% = 2.67% of

the resistors will be accepted although
the value is greater than 43 due to
measurement limitation
President University

Erwin Sitompul

PBST 8/24

Chapter 6.4

Applications of the Normal Distribution

Applications of the Normal Distribution

The average grade for an exam is 74, and the standard deviation is
7. If 12% of the class are given As, and the grade are curved to
follow a normal distribution, what is the lowest possible A and the
highest possible B?
P ( Z z ) 0.12
P ( Z z ) 1 P( Z z ) 1 0.12 0.88

z 1.175
x z 74 (1.175)(7) 82.225
President University

Lowest possible A is 83
Highest possible B is 82

Erwin Sitompul

PBST 8/25

Probability and Statistics

Homework 7A
1. Suppose the current measurements in a strip of wire are assumed to
follow a normal distribution with a mean of 10 milliamperes and a
variance of 4 milliamperes2. (a) What is the probability that a
measurement will exceed 13 milliamperes? (b) Determine the value for
which the probability that a current measurement is below this value is
98%. (Mo.E4.13-14 p.113)
2. A lawyer commutes daily from his suburban home to midtown office. The
average time for a one-way trip is 24 minutes, with a standard deviation
of 3.8 minutes. Assume the distribution of trip times to be normally
distributed. (a) If the office opens at 9:00 A.M. and the lawyer leaves his
house at 8:45 A.M. daily, what percentage of the time is he late for work?
(b) Find the probability that 2 of the next 3 trips will take at least 1/2
hour. (Wa.6.15 s.186)

President University

Erwin Sitompul

PBST 8/26