COMPARISON BETWEEN MASTER LEVEL AND DEGREE LEVEL

Master student Degree student

? ?
 Confidence
Intervals for the
mean
Estimation

 One aspect of inferential statistics

is estimation, which is the process
of estimating the value of a
parameter from information
obtained from sample.
Example:

 Suppose a college dean wishes to

estimate the average age of students
attending classes this semester. The dean
could select a random sample of 100
students and find the average age of
these students, say 22.3 years. From the
sample mean, the dean could infer that
the average age of all students is 22.3
years. This type of estimate is called
point estimate.
Point Estimate

 A point estimate is a specific

numerical value estimate of a
parameter. The best point estimate
of the population mean (μ) is the
sample mean (xbar).
Estimators

 Sample measures (statistics) are used to

estimate population measures
(parameter).
 These statistics are called estimators.
Three properties of a Good
Estimator
1. The estimator should be an
unbiased estimator.
 That is, the expected value or the mean of
the estimates obtained from samples of a
given size is equal to the parameter being
estimated.
Three properties of a Good
Estimator
2. The estimator should be consistent.
 For a consistent estimator, as a sample size
increases, the value of the estimator
approaches the value of the parameter
estimated.
Three properties of a Good
Estimator
3. The estimator should be a relatively
efficient estimator.
 That is, of all the statistics that can be used
to estimate a parameter, the relatively
efficient estimator has the smallest variance.
 But you ever say….

“ my weight is 55kg but easy to loose and

put on weight around 2 to 3 kg”
Interval estimate

 An interval estimate of a parameter is an

interval or a range of values used to
estimate the parameter. This estimate
may or may not contain the value of
parameter being estimated.
 For example: an interval estimate age for
the average student age
26.9 < μ < 27.7, or 27.3 + 0.4 years
Confidence level

 The confidence level of an interval

estimate of a parameter is the probability
that the interval estimate will contain the
parameter.
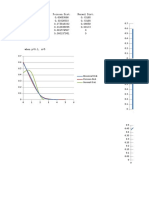
Confidence intervals provide both
the location and precision of a
measure: For example, the graphs
below show the 95% confidence
intervals around the average System
Usability Scale (SUS) score. The only
difference between the graphs is the
sample size. Even though they both
show the same location (a mean score
of 83), the one on the right has a
larger sample size (60), making it a
more precise estimate of the
population SUS score than the sample
with only 12.
Confidence interval

 A confidence interval is a specific interval

estimate of a parameter determined by
using data obtained from a sample and by
using the specific confidence level of the
estimate.
 Three common confidence level used:
90 %, 95 % and 99% confidence level
Confidence Interval

 Confidence intervals make a reasoned statement

about the true mean of a population based on a
random sample. When taking the mean (X) of a
random population sample; most likely, the mean
of that sample will not be the true mean of the
population ( µ ), but rather an estimate. The
confidence interval represents a range of values
around the sample mean that include the true
mean.
Confidence Intervals

 Confidence intervals are written with a

percentage; what does this percentage
represent?
 If the researcher were to take 100 random
samples with a 95% confidence interval for
each sample, then he or she expects that for
95 of the 100 samples (95%), the range of
values produced by the confidence interval
procedure will include the true mean of the
population. Although the researcher in
practice only has a single sample, the
researcher is confident that their interval
contains the true mean due to the process
used to calculate the confidence interval.
Formula for the Confidence Interval
of the Mean for a specific α

 xbar – zα/2 (σ/√n) < μ < xbar + zα/2 (σ/√n)

For 95 % confidence interval, zα/2 = 1.96;

and for 99% confidence interval, zα/2 = 2.58
Maximum error of estimate

 The term zα/2 (σ/√n) is called the

maximum error of estimate. For specific
value, say α= 0.05, 95 % of the sample
mean will fall within this error on either
side of the population mean.
 The maximum error of estimate is the
maximum likely difference between the
point estimate of a parameter and the
actual value of the parameter.
95 % Confidence Interval
Example:

 The dean of a faculty wishes to estimate the

average age of the students enrolled. From past
studies, the standard deviation is known to be 2
years. A sample of 50 students is selected, and the
mean is found to be 23.2 years. Find the 95%
confidence interval of the population mean.
 Solution:
 Since the 95% confidence interval is desired, zα/2 = 1.96. Hence
substituting in the formula
 xbar – zα/2 (σ/√n) < μ < xbar + zα/2 (σ/√n)
We get
23.2 – 1.96 (2/√50) < μ< 23.2 + 1.96 (2/√50)
23.2-0.6 < μ< 23.2 + 0.6
22.6 < μ< 23.8 or 23.2 + 0.6 years
Hence, the dean can say, with 95% confidence, that the
average age of students is between 22.6 and 23.8
years, based on 50 students.
Exercise:

A certain medication is known to

increase the pulse rate of its
users. The standard deviation of
the pulse rate is known to be 5
beats per minutes. A sample of
30 users had an average pulse
rate of 104 beats per minutes.
Find the 99 % confidence
interval of the true mean.
Solution:

 Since the 99% confidence interval is desired,

zα/2 = 2.58. Hence substituting in the formula
 xbar – zα/2 (σ/√n) < μ < xbar + zα/2 (σ/√n)
We get
104 – 2.58 (5/√30) < μ< 104 + 2.58 (5/√30)
104-2.4 < μ< 104 + 2.4
101.6< μ< 106.4
rounded to 102< μ< 106 or 104 + 2

Hence, one can be 99% confidence that the mean pulse

rate of all users of the medication is between 102
and 106 beats per minutes, based on a sample of 30
users.
Finding α/2 for 98%
Confidence Interval
 The Greek letter α represents the total of the areas in
both tails of the normal distribution.
 The value α is found by subtracting the decimal
equivalent of the desired confidence level from 1.
 Then α/2 is found by dividing α by 2.
Finding α/2 for 98%
Confidence Interval
Finding α/2 for 98%
Confidence Interval
 Once α/2 is found the corresponding zα/2 value can be
found.
 To get zα/2 value with 98% confidence interval, subtract
0.01 from 0.500 to get 0.4900.
 Next get the area that is closest to 0.4900 (in this case
0.4901) in Table E.
 Finding α/2 for a 98% Confidence
Interval

 The corresponding z value is 2.33

Exercise:

The following data represent a sample of the

assets (in millions of dollars) of 30 credit in
southwestern Pennsylvania. Find the 90% of
the mean.
$12.23 $16.56 $4.39
2.89 1.24 2.17
13.19 9.16 1.42
73.25 1.91 14.64
11.59 6.69 1.06
8.74 3.17 18.13
7.92 4.78 16.85
40.22 2.42 21.58
5.01 1.47 12.24
2.27 12.77 2.76
Solution:

 Mean, xbar = 11.091

 Standard deviation, s = 14.405
 α= 1 -0.90 = 0.10 and α/2 = 0.10/2 = 0.05.
 The corresponding z value obtained from Table is 1.65 (
a more precise value is 1.645)
Solution:

 Substituting in the formula

 xbar – zα/2 (s/√n) < μ < xbar + zα/2 (s/√n)
 (s is used in place of σ when is unknown,
since n≥ 30)
 11.091 – 1.65(14.405/√30)<μ< 11.091 +
1.65(14.405/ √30)
 11.091 – 4.339 < μ < 11.091 + 4.339
 6.752 < μ < 15.430
 Hence, one can be 90% confident that the
population mean of the assets of all the
credit unions is between $6.752 million and
15.430 million, based on a sample 30 credit
unions.
Thank You