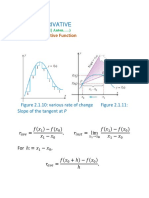
DERIVATIVE OF FUNCTION OF A FUNCTION

[CHAIN RULE]
If y = f(u) and u = g(x) are differentiable function of u and x respectively,
then

If y = f(u), u = g(w), w = h(x) are differentiable functions, then by chain

rule, we have

= . . .

If u is a differentiable function of x, then by chain rule, we have

( )

= n 1

EXAMPLE 1. If y = 2 + 2 and u = 3 1, then find the derivative of y

w.r.t. x using the chain rule.
SOLUTION:

We have

y = 2 + 2
u = 3 1

..(1)
.........(2)

Using chain rule,

(1)

(2)

2 + 2 = 2
3 1 = 3 2 1

= 2 3 2 1 = 2( 3 1)(3 2 1)

= 6 5 8 3 6 2 + 2 + 2.

EXAMPLE 2. Find by using chain rule for the following function:

=

1
,
1+

SOLUTION: we have

2
1 2
1
=
,
1+

=
=

Also,

1+

2
1 2

1 (1)

(1+)2
1+ 1 1 .1
(1+)2
1 2 .

2 2

(1 2 )2

1 2 22(2)
(1 2 )2

(1+)

2
(1+)2

(1 2 )

2(1+ 2 )
(1 2 )2

By Chain rule,

2
2 2
)
12
4(1+ 2 )

(1+

(1+)2

2(1+ 2 )
.
(1 2 )2

2 1+ 2

4(1 2 )2 (1+ 2 )
(1 2 +2)2

. (1 2 )2 =

= (1+2 2 )2

EXAMPLE 3. differentiate the following function w.r.t. x: ( + ( 2 +2 )

SOLUTION: let = ( + ( 2 +2 )

= ( + 2 + 2 )1 .

= ( + 2 + 2 )1 1 +

+ 2 + 2 )

( 2

+ 2 )1/2

1
2

= ( + 2 + 2 )1 1 + ( 2 + 2 )1/2 .
= ( + 2 + 2 )1 1 +

= ( +

2 )1

(+ 2 +2 )
2 +2

1
2 2 +2

2 +2 +
2 +2

(2 + 0)

( 2

+ 2 )

DIFFERENTIATION OF FUNCTIONS EXPRESSED

IN
PARAMETRIC FORM
Or PARAMETRIC DIFFERENTIATION
when two variables x and y are both functions of a third variable (which is
called as parameter), then the equations are called parametric equations.
Let = () and = g(t) where t is a parameter.

Then,
For example find

when = 2 = 2a 2

Solution: we have = 2 = 2a 2

= 3 2 ,

= 4

4
3 2

4
3

EXAMPLE 1. Find

when =

we have =

SOLUTION:

3
,
1+ 3

3 2
.
1+ 3

3 2
.
1+ 3

1+ 3 33(0+3 2 )

(by using quotient formula)

(1+ 3 )2

3+3 3 9 3
(1+ 3 )2

3
,
1+ 3

3(12 3)
(1+ 3 )2

1+ 3 .63 2
(1+ 3 )2

6+6 4 9 4
(1+ 3 )2

3(2 3 )
(1+ 3 )2

3(23 )
(1+3 )2
3(123)
(1+3 )2

3(2 3 )
(1+ 3 )2

(1+ 3 )2
3(12 3 )

(2 3 )
12 3

(by using quotient formula)

1+log

EXAMPLE 3. If =
, =
2

2
=
= 2
+1

SOLUTION: we have =

2 . (1+log ).2
( 2 )2

(1+2 log )
4
3+2 log

.2. 3+2 log .1

2
1+2 log

> 0. then show that

1+log
2

=
Now

3+2 log
,

22 log
4

(By using quotient formula)

1+2 log
3

1+2 log

232 log
2

1+2 log

(By using quotient formula)

L.H.S. =

3+2 log

= 3 + 2 log

R.H.S. = 2( )2 + 1
=2

1+log
2

2 + 1 = 2 + 2 log + 1

= 3 + 2 log

L.H.S. = R.H.S.

Hence y

= 2( )2 + 1.